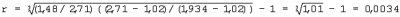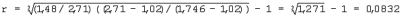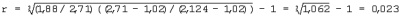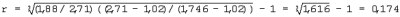Патент на изобретение №2247984
|
||||||||||||||||||||||||||
(54) СПОСОБ ОПРЕДЕЛЕНИЯ ГЕОМЕТРИЧЕСКИХ СИМПЛЕКСОВ В СТРУКТУРЕ ДИСПЕРГИРОВАННЫХ СИСТЕМ
(57) Реферат:
Изобретение относится к области испытания свойств материалов и может быть использовано в процессе проектирования оптимального состава композиций строительного назначения. В способе определения геометрического симплекса в структуре диспергированных систем, содержащих твердую и жидкую фазы, определяют объемную массу сухой твердой фазы, плотность жидкой и сухой твердой фаз, массовое соотношение жидкой и сухой твердой фаз, плотность диспергированной системы по формуле и при Nж/т больше N величины геометрических симплексов рассчитывают по формуле: где r = hж/dcp.т, геометрический симплекс, безразмерная величина; hж – толщина прослоек жидкой фазы между телами твердой фазы, мм; dcp.т – средние линейные размеры тел твердой фазы, мм;
Изобретение относится к области испытаний и определения свойств материалов и может быть использовано в процессе проектирования оптимального состава композиций строительного назначения. Известно, что структура наряду с составом системы влияет на свойства композиций и строительных материалов, производимых на их основе (Общий курс строительных материалов. Учебное пособие для вузов. Под ред. И.А.Рыбьева. М.: Высшая школа. 1987. 584 с.). Элементами структуры диспергированных систем являются твердые тела различной формы и размеров, а также микрообъемы и прослойки жидкой фазы между ними. Массовое отношение жидкой и твердой фаз в диспергированной системе (Nж/т=Ж, кг/Т, кг) количественно характеризует состав системы и относится к категории критериальных величин. Геометрические симплексы (отношение линейных размеров толщины прослоек жидкой и тел твердой фаз) в диспергированных системах количественно характеризуют их структурные особенности и также относятся к категории критериальных величин. Геометрические симплексы определяют технологические свойства композиций (подвижность, текучесть, удобоукладываемость, характеристики формования). При hж/dср.т, стремящемся к нулю, в системе начинают преобладать сдвиговые напряжения, определяемые силами контактного трения между твердыми телами. При hж/dср.т, стремящемся к единице, в системе формируются прослойки жидкой фазы, соизмеримые с линейными размерами тел твердой фазы. При этом текучие свойства диспергированной системы повышаются и определяются в основном вязкостью жидкой фазы, содержащей в своем составе микроскопические частицы коллоидного типа, находящиеся в состоянии броуновского движения и не обладающие седиментационной способностью. Физико-механические характеристики материалов, изготовленных с использованием композиций диспергированного характера, также определяются геометрическими симплексами. Общеизвестно, что при формировании пленок жидкости, соизмеримых с размерами молекул, резко изменяются свойства жидкости. Они определяются силами физико-химического взаимодействия жидкости с поверхностью твердого тела. Геометрические симплексы, выражающие пропорциональные зависимости между линейными величинами (r=hж/dср.т), используются для определения объемных коэффициентов раздвижки в теории упаковки твердых тел в различных жидких средах. Явление раздвижки сопровождается увеличением объема системы и его действие имеет радиальное направление. Таким образом, геометрические симплексы являются носителями не только количественной, но и векторной информации. В основе создания изобретения лежит задача по разработке такого способа, который позволяет унифицировать независимо от природы жидкой и твердой фаз определение геометрических симплексов в структуре диспергированных систем, снизить объем испытаний исходных материалов, повысить точность определяемых величин, а также обеспечить возможность проектирования сложных по составу композиций строительного назначения с использованием величин, определяемых по заявленному способу. Технический результат выражается в том, что используют объемно-массовые характеристики и массовое отношение жидкой и твердой фаз, являющихся компонентами диспергированнных систем. Поставленная задача решается тем, что способ определения геометрического симплекса в структуре диспергированных систем, содержащих твердую и жидкую фазы, характеризующийся тем, что определяют объемную массу сухой твердой фазы, плотность жидкой и сухой твердой фаз, массовое соотношение жидкой и сухой твердой фаз, плотность диспергированной системы по формуле и при Nж/т больше N величины геометрических симплексов рассчитывают по формуле: где r=hж/dcp.т, геометрический симплекс, безразмерная величина, hж – толщина прослоек жидкой фазы между телами твердой фазы, мм; dcp.т – средние линейные размеры тел твердой фазы, мм;
Nж/т – массовое соотношение жидкой и сухой твердой фаз, безразмерная величина, N – величина, рассчитываемая по формуле: N= Рдс=((1+Nж/т)· Способ осуществляется следующим образом. Пример 1. Для определения геометрических симплексов в цементном тесте определяют плотность цемента, она равна Для приведенных данных водоцементное отношение составит величину N= N=(3,06-1,45)/(1,45· 3,06)=1, 610/4,437=0,363, безразмерная величина. Определяют плотность цементного теста при значениях N больше 0,363. При N=0,370 плотность цементного теста равна:
При dcp.ц=0,002 мм (2 мкм) hв=0,002 мм· 0, 0037=0,0000074 мм (0,0074 мкм). При dср.ц=0,008 мм (8 мкм) hв=0,008 мм· 0, 0037=0,0000296 мм (0,0296 мкм). При N=0,4 плотность цементного теста равна
При dcp.ц=0,002 мм (2 мкм) hв=0,002 мм· 0,0177=0,0000354 мм (0,0354 мкм). При dcp.ц=0,008 мм (8 мкм) hв=0,008 мм· 0,0177=0,000142 мм (0,142 мкм). Пример 2. Исходные данные аналогичны примеру 1. Используют цемент с объемной массой N=( Определяют плотность цементного теста при значениях N больше 0,287. При N=0,290 плотность цементного теста равна:
При dср.ц=0,002 мм (2 мкм) hв=0,002 мм· 0,138=0,0000354 мм (0,0354 мкм). При dср.ц=0,008 мм (8 мкм) hв=0,008 мм· 0,138=0,0011 мм (1,1 мкм) При N=0,4 плотность цементного теста равна
При dcp.ц=0,002 мм (2 мкм) hв=0,002 мм· 0,058=0, 000116 мм (0,116 мкм). При dcp.ц=0,008 мм (8 мкм) hв=0,008 мм· 0,058=0,000464 мм (1,1 мкм). Пример 3. Для определения геометрических симплексов в асфальтовом вяжущем веществе определяют плотность минерального порошка (известняковая мука), она равна Для приведенных данных битумоминеральное отношение составит величину, равную N=1,02((2,71-1,48)/(1,48-2,71))=1,02 (1,230/4,011)=0,313. Определяют плотность асфальтового вяжущего вещества (ABB) при значениях N больше 0,313. При N=0,320 плотность ABB равна:
При dcp.мп=0,002 мм (2 мкм) hб=0,002 мм· 0,0034=0,0000068 мм (0,0068 мкм). При dcp.мп=0,008 мм (8 мкм) hб=0,008 мм· 0,0034=0,0000272 мм (0,0272 мкм). При N=0,5 плотность асфальтового вяжущего вещества равна Равв=((1+0,5)· 1,02· 2,71)/(0,5· 2,71+1,02)=1,746 г/см3, а геометрический симплекс равен При dcp.мп=0,002 мм (2 мкм) hб=0,002 мм· 0,0832=0,000116 мм (0,116 мкм). При dcp.мп=0,008 мм (8 мкм) hб=0,008 мм· 0,0832=0,000666 мм (0,666 мкм). Пример 4. Исходные данные аналогичны примеру 3. Используют минеральный порошок, подвергнутый уплотнению при давлении 40 МПа, объемная масса уплотненного порошка равна N= Определяют плотность асфальтового вяжущего вещества (ABB) при значениях N больше 0,166. При N=0,2 плотность АВВ равна:
При dcp.мп=0,002 мм (2 мкм) hВ=0,002 мм· 0,023=0,000046 мм (0,046 мкм). При dcp.мп=0,008 мм (8 мкм) hв=0,008 мм· 0,023=0,000184 мм (0,184 мкм). При N=0,5 плотность ABB равна
а геометрический симплекс равен При dcp.мп=0,002 мм (2 мкм) hб=0,002 мм· 0,174=0,000348 мм (0,348 мкм). При dcp.мп=0,008 мм (8 мкм) hб=0,008 мм· 0,174=0,00139 мм (1,39 мкм). Заявленный способ определения геометрических симплексов в структуре диспергированных систем обладает универсальностью и применим к любым системам, состоящим из жидкой и твердой фаз. Физические величины, количественно характеризующие свойства твердой и жидкой фаз, можно получить в любой производственной лаборатории строительного или дорожно-строительного профиля. Для определения показателей физических свойств исходных компонентов используются стандартные методики испытания дорожно-строительных материалов. Геометрические симплексы как мера количественной оценки линейных величин элементов структуры диспергированных систем используются для определения объемных коэффициентов раздвижки (разбавления) в процессе проектирования оптимальных составов бетонных и асфальтобетонных смесей с заданным комплексом физико-механических, технологических и эксплуатационных свойств.
Формула изобретения
Способ определения геометрического симплекса в структуре диспергированных систем, содержащих твердую и жидкую фазы, характеризующийся тем, что определяют объемную массу сухой твердой фазы, плотность жидкой и сухой твердой фаз, массовое соотношение жидкой и сухой твердой фаз, плотность диспергированной системы по формуле и при Nж/т больше N величины геометрических симплексов рассчитывают по формуле где r = hж/dcp.т, геометрический симплекс, безразмерная величина, hж – толщина прослоек жидкой фазы между телами твердой фазы, мм; dcp.т – средние линейные размеры тел твердой фазы, мм;
Nж/т – массовое соотношение жидкой и сухой твердой фаз, безразмерная величина, N – величина, рассчитываемая по формуле N =
MM4A – Досрочное прекращение действия патента СССР или патента Российской Федерации на изобретение из-за неуплаты в установленный срок пошлины за поддержание патента в силе
Дата прекращения действия патента: 16.12.2005
Извещение опубликовано: 20.08.2007 БИ: 23/2007
|
||||||||||||||||||||||||||

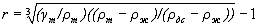 ,
, дс – плотность диспергированной системы, кг/м3, определяемая по формуле:
дс – плотность диспергированной системы, кг/м3, определяемая по формуле:  т – объемная масса сухой твердой фазы, г/см3;
т – объемная масса сухой твердой фазы, г/см3; 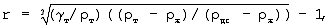
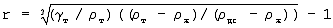 ,безразмерная величина.
,безразмерная величина.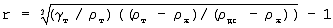 , равен
, равен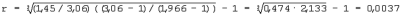
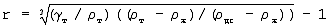 равен
равен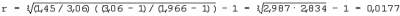
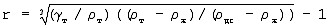 равен
равен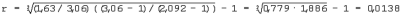
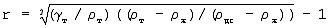 равен
равен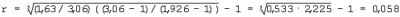
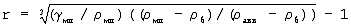 , равен
, равен